Maxwell's Equations

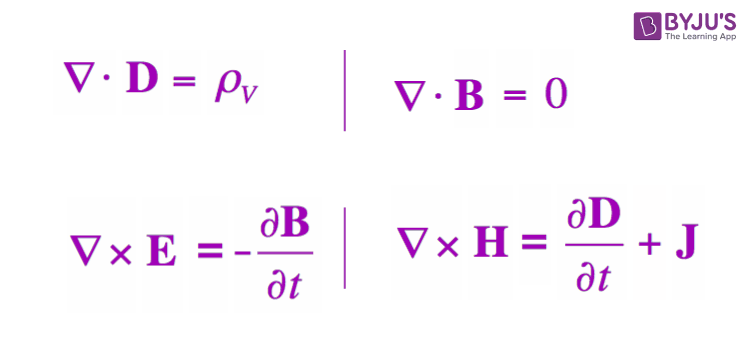
Maxwell was the first person to calculate the speed of propagation of electromagnetic waves, which was the same as the speed of light and came to the conclusion that EM waves and visible light are similar. These are the set of partial differential equations that form the foundation of classical electrodynamics, electric circuits and classical optics along with Lorentz force law. These fields highlight modern communication and electrical technologies.

Maxwell First Equation

Maxwell’s first equation is based on the Gauss law of electrostatic, which states that “when a closed surface integral of electric flux density is always equal to charge enclosed over that surface”.

Maxwell Second Equation

Maxwell second equation is based on Gauss law on magnetostatics. Gauss law on magnetostatics states that “closed surface integral of magnetic flux density is always equal to total scalar magnetic flux enclosed within that surface of any shape or size lying in any medium.”

Maxwell Third Equation

Statement: Time-varying magnetic field will always produce an electric field. Maxwell’s 3rd equation is derived from Faraday’s laws of Electromagnetic Induction. It states that “Whenever there are n-turns of conducting coil in a closed path placed in a time-varying magnetic field, an alternating electromotive force gets induced in each coil.” Lenz’s law gives this. Which states, ” An induced electromotive force always opposes the time-varying magnetic flux.”

Maxwell’s Fourth Equation

It is based on Ampere’s circuit law. To understand Maxwell’s fourth equation, it is crucial to understand Ampere’s circuit law, Consider a wire of a current-carrying conductor with the current I. Since there is an electric field, there has to be a magnetic field vector around it. Ampere’s circuit law states that “The closed line integral of magnetic field vector is always equal to the total amount of scalar electric field enclosed within the path of any shape”, which means the current flowing along the wire(which is a scalar quantity) is equal to the magnetic field vector (which is a vector quantity)

For more information Wikipedia